
When discussing genetics, people often bandy about the phrase ‘inbreeding coefficient’- essentially a mathematical way of expressing how much inbreeding there is in someone’s ancestry. As an example, Charles II of Spain had an inbreeding coefficient of 0.254, which is higher than the 0.25 which results from the children of a sibling or parent-child union. I haven’t been able to find a public-domain image of Charles II’s ancestry, but have a look at his Wikipedia page if you’re interested in the detail. Sufficed to say, Charles II was not a healthy man, dying at the age of just 39. He had been unable to walk until the age of 8 to 10 and in Spain was known as ‘the Bewitched‘.
There are people who have calculated figures like this for other people. For example, there is a blog post which informed me that Danaerys Targaryen, one of the (many!) point-of-view characters of Game of Thrones would have a coefficient of 0.375. But how is this figure calculated?
Although I haven’t been able to figure out exactly how it works for more complicated puzzles such as the ones we’re discussing, I’m going to take you through the process for some simpler examples, using a method I learned from a blog I’m putting a link to here. Please note that this is a guide to the method, rather than a discussion of the impacts of inbreeding on particular families. However, if this is something people would be interested in, I have found some papers which reconstruct the diseases suffered from by the Ptolemies of Egypt using their symptoms, so if this is something people would be interested in, feel free to let me know in the comments.
So, let’s try and work out the inbreeding coefficient of these two individuals:
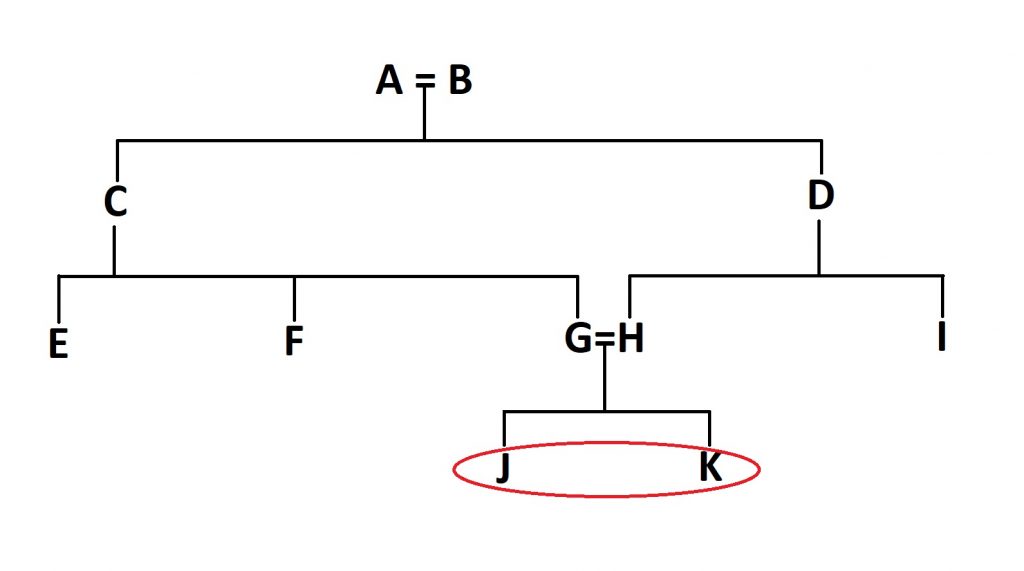
The first thing we need to do is to find the first inbred individuals in the family tree- in this case, J and K, as their parents (G and H) share a set of grandparents and therefore common ancestors. Once we’ve found them, we need to count the number of steps between the two parents:
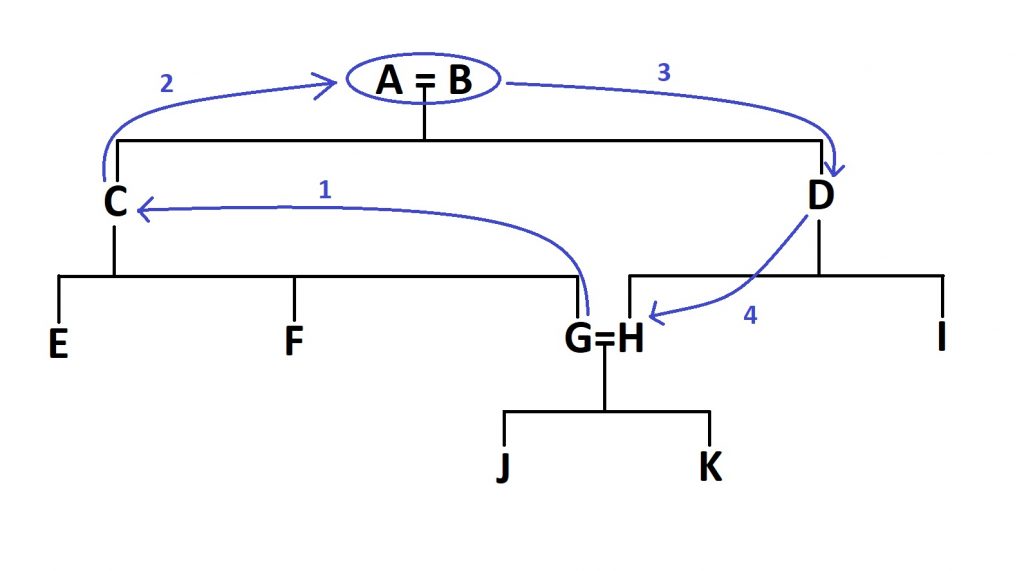
In this case, we would need four steps, through the grandparents (A and B) to get from G to H, as shown in Figure 2.
Now the first bit of the equation. Take the number of steps and add one. You might now be breathing a sight of relief, but we’re sadly not done after this point. Now you need to raise 0.5 to the power of this new number. So for our example above, it is (0.5)^5, or 1/32, or 0.03125. This new number needs to be doubled, as this exact same route can be taken through both parents (this wouldn’t be the case if they were related through half-siblings, for example). So, the number you end up with is 0.0625, or 6.25%. So, the coefficient of inbreeding for two individuals born from a first-cousin union is 6.25%, or 1/16th.
But we can go further. What if the children of J and K (let’s call them M and N) marry and have children? How will this impact the inbreeding coefficient of individual P?
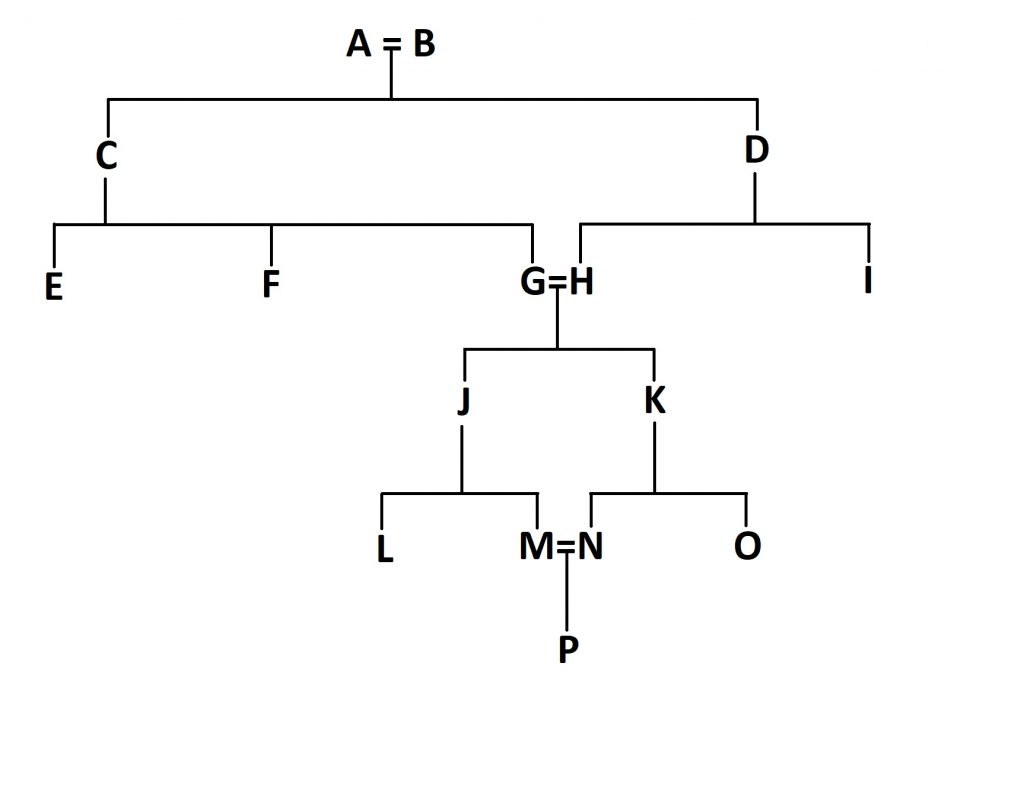
First off, go through the same process again for these new parents, M and N. You end up with 1/32 for this loop, as you did last time. Double it as before and end up with 1/16th.
But now, we need to go through some more steps. We need to add one to this 1/16th we got last time to get 17/16. This might not seem logical at the moment, but bear with me.
The reason we’re doing this is that this second set of parents don’t start off with a clean slate, if you like- they are inbred themselves, given the marriage of individuals G and H way back in the day. So, the equation for this second set of inbred parents is accordingly more complicated. You need to multiply the number you would otherwise get (1/16th for our purposes) by the 17/16 you just got and then multiply all of that by 2. Why double it? Well, because the number of routes you can take to the original common ancestors A and B has doubled; both M and N can trace their lineage back to them via both G and H. To summarise that logical jump, here’s a diagram:
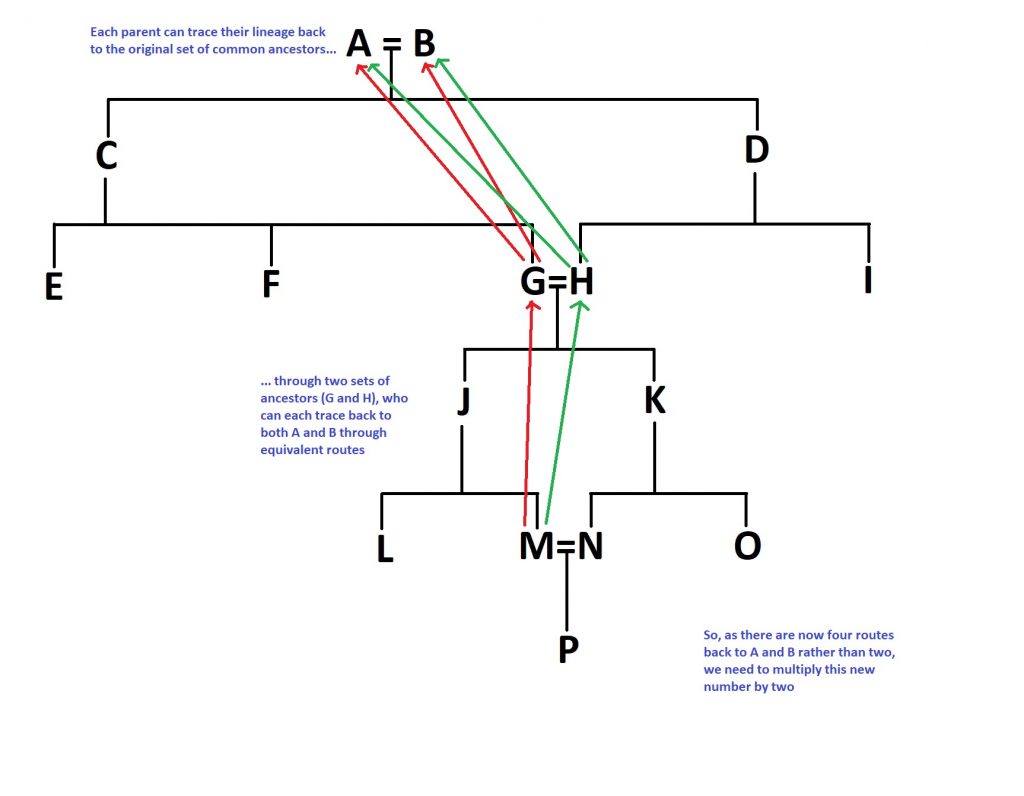
Now the final step, I promise. We now need to add these two numbers together- the original number we got for G and H, and the second number we’ve just calculated for P. So, adding this all together, you get:
1/16 + (1/16 * 17/16 * 2) = 0.1953125, which rounds to 0.195, or 19.5%.
This whole process can be summarised as:
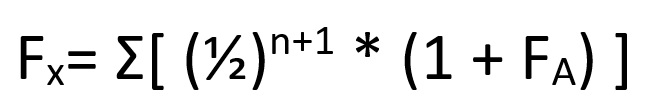
Where (1 + F(A)) refers to the inbreeding coefficient adjusted for the already inbred parents- in our case, the 17/16 we calculated earlier.
Here’s hoping that I’ve managed to explain all of this correctly, as truth be told it took me quite a while to get my head around it. If not, feel free to let me know and I’ll be sure to update this post when I am able to.
- Image Credit:
- Image: Pixabay
- User: EliasSch
- Featured image: Man Dna Spiral – Free image on Pixabay
- Image labelled for reuse
- No changes have been made
